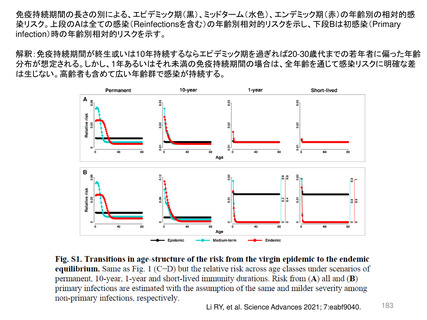
資料3-3 西浦先生提出資料 (177 ページ)
出典
| 公開元URL | https://www.mhlw.go.jp/stf/seisakunitsuite/bunya/0000121431_00348.html |
| 出典情報 | 新型コロナウイルス感染症対策アドバイザリーボード(第95回 8/18)《厚生労働省》 |
ページ画像
プレーンテキスト
資料テキストはコンピュータによる自動処理で生成されており、完全に資料と一致しない場合があります。
テキストをコピーしてご利用いただく際は資料と付け合わせてご確認ください。
常微分方程式dI/dt=0を解いてIをパラメータだけで記述することにより、平衡状態におけるPrevalence(人口中の
感染者比率)について理解することができる。平衡状態の解は以下の通りである。
𝐼∗ =
上記について、基本再生産数R0を1~
10の範囲で数値解を検討したものが右図
である。平均世代時間についてDd=5日
間と仮定した(オミクロン株の平均世代時
間はこれより若干短い可能性があり、そ
の場合は上式のDdが短くなり、I*の解が
ここで示すよりも小さくなる)。
0
𝐷
1 + 𝐷𝑖
𝑑
7
平均免疫持続期間
immunity = 10 weeks
immunity = 20 weeks
immunity = 50 weeks
6
平衡状態での感染者割合(%)
【考察】
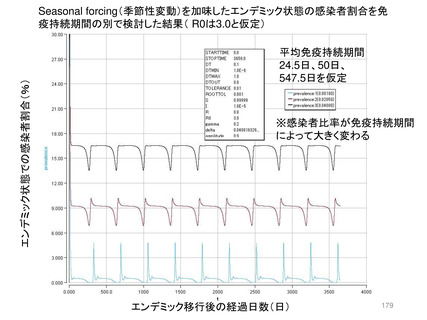
重要な解釈として、(1)エンデミック化し
た定常状態ではR0よりも免疫持続期間
DiがPrevalenceを大きく左右し、疫学的
に重要な役割を果たすことが挙げられる。
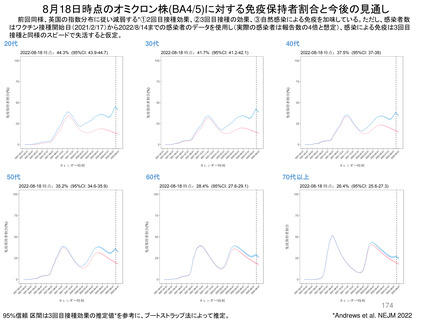
また、(2)英国におけるOffice of
National Statisticsのサーベイでは
BA.1/2及びBA.4/5の流行で2~8%程度
の感染者割合で推移した。感染予防効果
の平均免疫持続期間が文献値で得られ
ている3-4カ月程度と仮定すると、概ね平
衡解の数値と観察値が一致する。
免疫持続期間が1年未満だとすると、
COVID-19のエンデミック化は、数%以上
の感染者比率の流行が続くことを受け入
れるものである。
1
1−𝑅
5
4
3
2
1
0
0
1
2
3
4
5
6
R0 (基本再生産数)
7
8
9
177
10