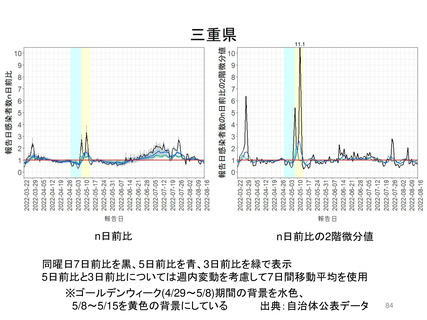
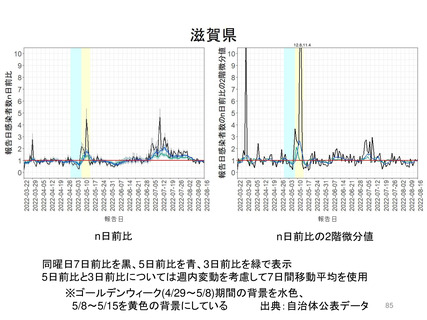
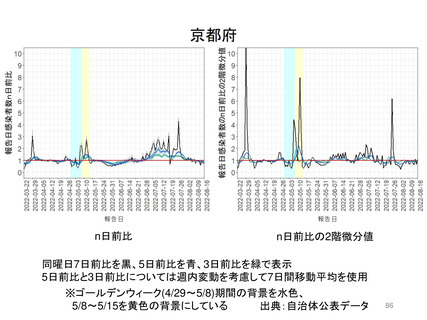
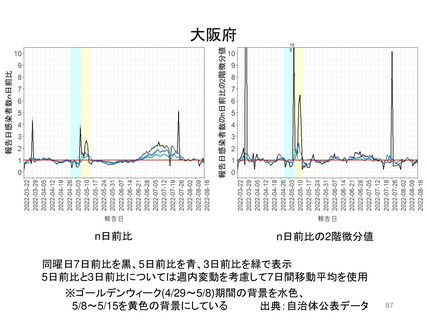
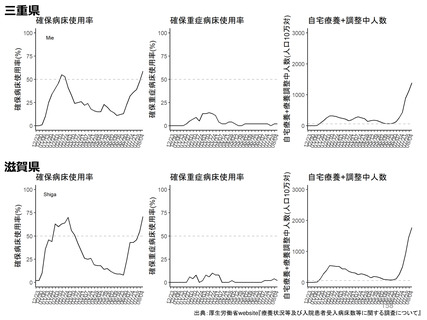
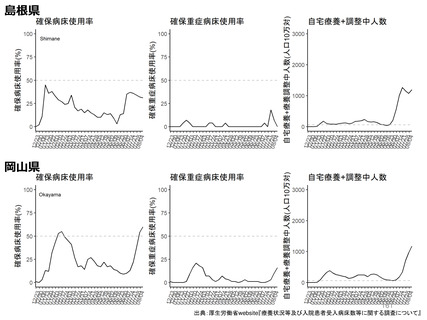
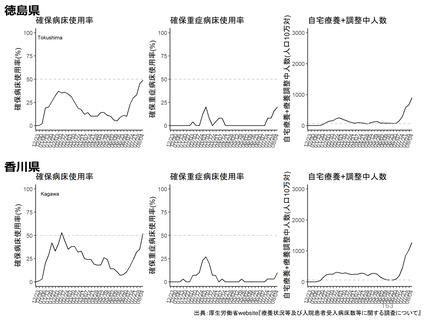
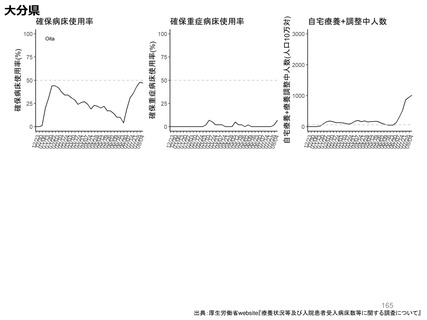
資料3-3 西浦先生提出資料 (180 ページ)
出典
| 公開元URL | https://www.mhlw.go.jp/stf/seisakunitsuite/bunya/0000121431_00348.html |
| 出典情報 | 新型コロナウイルス感染症対策アドバイザリーボード(第95回 8/18)《厚生労働省》 |
ページ画像
プレーンテキスト
資料テキストはコンピュータによる自動処理で生成されており、完全に資料と一致しない場合があります。
テキストをコピーしてご利用いただく際は資料と付け合わせてご確認ください。
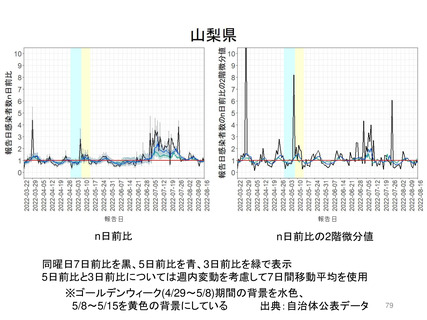
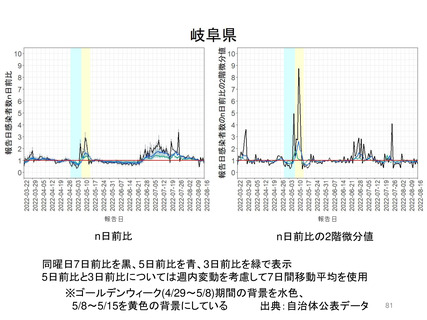
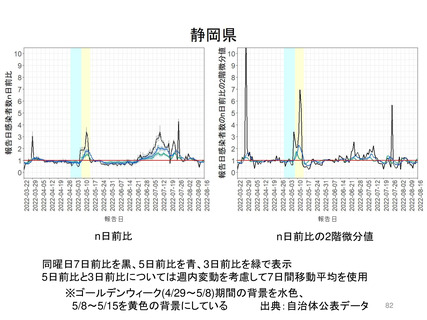
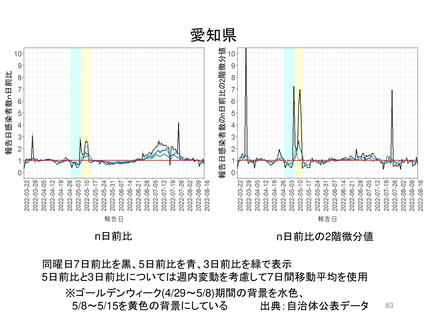
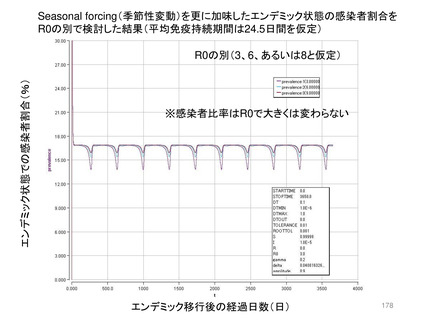
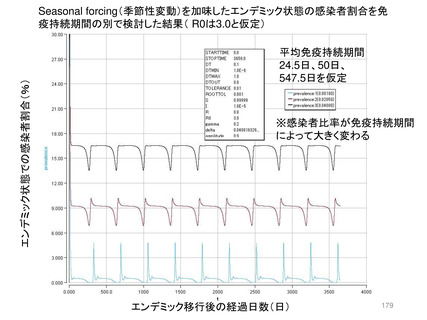
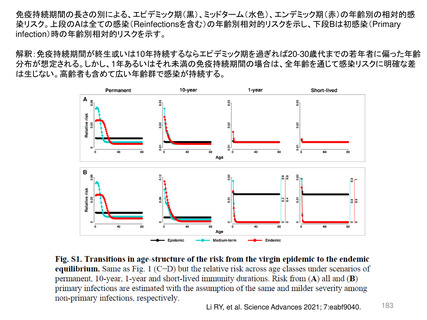
Seasonal forcingを加味した場合もエンデミック状態に関する定性的な見解は大きく異ならない。「R0
よりも免疫持続期間がPrevalenceを大きく左右する」。但し、季節性を加味した数値計算結果のほうが、
英国ONSサーベイで観察された2~8%を再現するためには免疫持続期間が長い必要があり、ここで
は平均免疫持続期間が概ね1年から2年(前ページでは1.5年)程度であれば、10%未満のPrevalence
が再現されることがわかる。現状、免疫保持期間が具体的にどれくらいの長さであるのかは更なる研究
知見を要する。
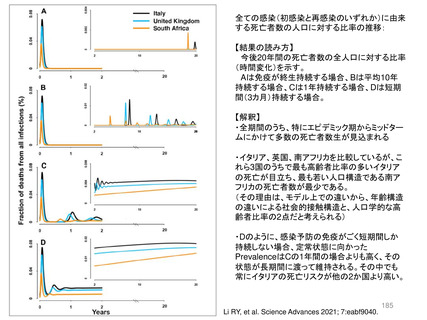
数%~10%台と言われるCOVID-19のエンデミック状態のSeasonal dynamicsは、季節性インフル
エンザで議論されている0.1から0.3%台のPrevalence(Antigenic driftとWaningをあわせて上記モ
デルでDi=5年間としたとき)と比べて10倍程度高いレベルで推移することを意味する。つまり、感染レベ
ルは季節性インフルエンザのそれとは比較にならないくらい高い状態が継続する。
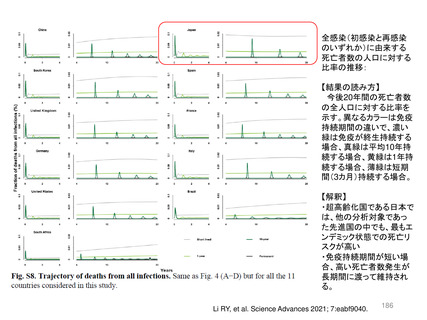
エンデミック化した後には、常に無視できないパーセンテージの感染者割合が認められることを示唆
する。
METHOD RK4
(参考)
常微分方程式モデルのコード
(Berkeley Madonna)とそのパラ
メータ、初期条件
※ここではSeasonal forcing あり
(振幅0.9)、平均感染性期間(平均
世代時間)5日、平均免疫持続期間
3.5週を仮定したものを示す。
Background demographic
dynamicsは簡略化しているが、出
生が多くなるとPrevalenceは高くな
る
RENAME TIME = t
STARTTIME = 0
STOPTIME = 3650
DT = 0.1
{Equation system}
d/dt(S) = -beta * S* I+ delta*R
d/dt(I) = beta * S* I - gamma * I
d/dt(R) = gamma* I - delta * R
prevalence = I*100
{parameters}
R0 = 3
gamma = 1/5
beta =
(R0/gamma)*(1+amplitude*SIN(2*pi*t/365))
delta = 1/(3.5*7)
amplitude = 0.9
{initial conditions}
init S = 0.99999
init I = 0.00001
init R = 0
180